Понятие о переменном токе
Предисловие.
Прежде чем начать разговор о счетчиках, вспомним что это приборы электрические, и в дальнейшем описании я буду бросаться всякими умными терминами. Конечно если у вас имеется электротехническое образование, то эту часть можно сразу пропустить. А если про электричество вы знаете только то, что если воткнуть утюг в розетку он начнет греться, то настоятельно рекомендую прочесть эту главу, чтобы потом не чувствовать себя чужим на всеобщем празднике жизни. Глава взята с сайта Воропаев Е.Г. "Электротехника", там еще много таких, рекомендую почитать для самообразования, написано вполне популярно (на уровне первого курса электротехнического техникума).
Итак:
Определение: Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.
![]() и измеряется в герцах (Гц). Величина
и измеряется в герцах (Гц). Величина ![]() называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду
называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду
Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом ''m'' (например, Im). Существует также понятие, действующего значения переменного тока (I). Количественно оно равно: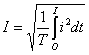
следует заметить, что действующее значение напряжения меньше максимального.
Переменный ток можно математически записать в виде:
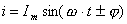
Здесь индекс выражает начальную фазу. Если синусоида начинается в точке пересечения осей координат, то = 0, тогда
![]()
Начальное значение тока может быть слева или справа от оси ординат. Тогда начальная фаза будет опережающей или отстающей.
1.2. СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА.
Электрический ток в проводниках непрерывно связан с магнитным и электрическими полями.
Элементы, характеризующие преобразование электромагнитной энергии в тепло, называются активными сопротивлениями (обозначаются R).
Элементы, связанные с наличием только магнитного поля, называются индуктивностями.
Элементы, связанные с наличием электрического поля, называются емкостями.
Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д.
Индуктивностью обладают катушки реле, обмотки электродвигателей и трансформаторов. Индуктивное сопротивление подчитывается по формуле:
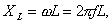
где L - индуктивность.
Емкостью обладают конденсаторы, длинные линии электропередачи и т.д.
Емкостное сопротивление подсчитывается по формуле:
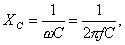
где С - емкость.
Реальные потребители электрической энергии могут иметь и комплексное значение сопротивлений. При наличии R и L значение суммарного сопротивления Z подсчитывается по формуле:
![]()
Аналогично ведется подсчет Z и для цепи R и С:
![]()
Потребители с R, L, C имеют суммарное сопротивление:
![]()
1.3. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ АКТИВНОГО СОПРОТИВЛЕНИЯ R,
КОНДЕНСАТОРА С И ИНДУКТИВНОСТИ L
Рассмотрим цепь с активным, индуктивным и емкостным сопротивлениями, включенными последовательно (рис. 1.3.1).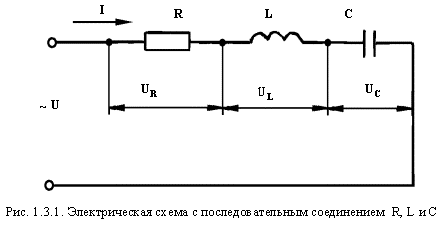
Для анализа схемы разложим напряжение сети U на три составляющие:
UR - падение напряжения на активном сопротивлении,
UL - падение напряжения на индуктивном сопротивлении,
UC - падение напряжения на емкостном сопротивлении.
Ток в цепи I будет общим для всех элементов:
![]()
Проверку производят по формуле:
![]()
Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I.
Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном - отстает от него на 90°.
Графически это можно показать на векторной диаграмме (рис. 1.3.2).
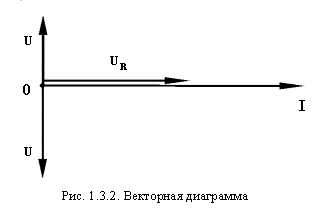
Изображенные выше три вектора падения напряжений можно геометрически сложить в один (рис. 1.3.3).
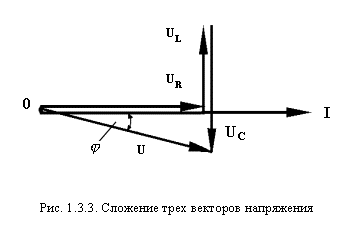
В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак.
Интересным является режим, когда = 0.
В этом случае ![]()
Такой режим работы схемы называется резонансом напряжений.
Полное сопротивление при резонансе напряжений имеет минимальное значение: ![]()
, и при заданном напряжении U ток I может достигнуть максимального значения.
Из условия ![]() определим резонансную частоту
определим резонансную частоту![]()
Явления резонанса напряжений широко используется в радиотехнике и в отдельных промышленных установках.
1.4. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРА И КАТУШКИ,
ОБЛАДАЮЩЕЙ АКТИВНЫМ СОПРОТИВЛЕНИЕМ И ИНДУКТИВНОСТЬЮ
Рассмотрим цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью (рис. 1.4.1).
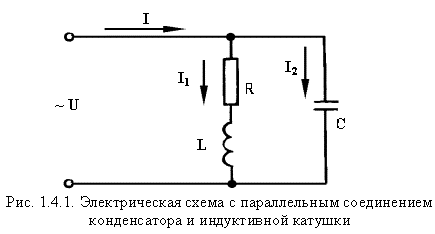
В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь - индуктивная катушка - обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z1 и ток I1 определяются по формуле:
![]() , где
, где ![]()
Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол .![]()
Покажем это на векторной диаграмме (рис. 1.4.2).
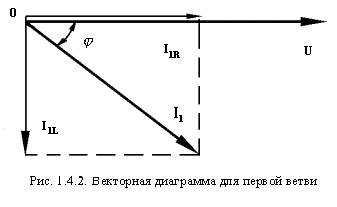
Спроецируем вектор тока I1 на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I1R, а вертикальная - I1L. Количественные значения этих составляющих будут равны:
![]() где
где ![]()
Во вторую ветвь включен конденсатор. Его сопротивление
![]()
Этот ток опережает по фазе напряжение на 90°.
Для определения тока I в неразветвленной части цепи воспользуемся формулой:
![]()
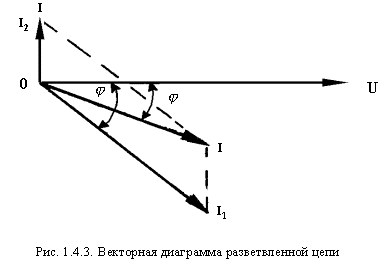
Его значение можно получить и графическим путем, сложив векторы I1 и I2 (рис. 1.4.3)
Угол сдвига между током и напряжением обозначим буквой j.
Здесь возможны различные режимы в работе цепи. При = +90° преобладающим будет емкостный ток, при = -90° - индуктивный.
Возможен режим, когда = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I1L = I2, т.е. при равенстве реактивных составляющих тока в ветвях.
На векторной диаграмме это будет выглядеть так (рис. 1.4.4):
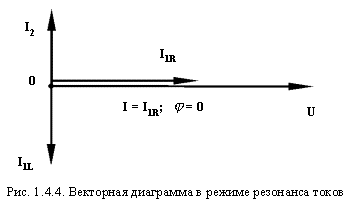
Такой режим называется резонансом токов. Также как в случае с резонансом на-пряжений, он широко применяется в радиотехнике.
Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosj для электроустановок. Известно, что cosj является технико-экономическим параметром в работе электроустановок. Определяется он по формуле:
![]() , где
, где
Р - активная мощность электроустановок, кВт,
S - полная мощность электроустановок, кВт.
На практике cosj определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgj .
Далее по таблицам находят и cosj.
Чем больше cosj, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosj приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosj, в сравнении с низким.
К мероприятиям по повышению cos относятся:
- недопущение холостых ходов электрооборудования,
- полная загрузка электродвигателей, трансформаторов и т.д.
Кроме этого, на cosj, положительно сказывается подключение к сети статических конденсаторов.
Created/Updated: 25.05.2018
 |
|